FAPO: Flawed-Aware Policy Optimization for Efficient and Reliable Reasoning

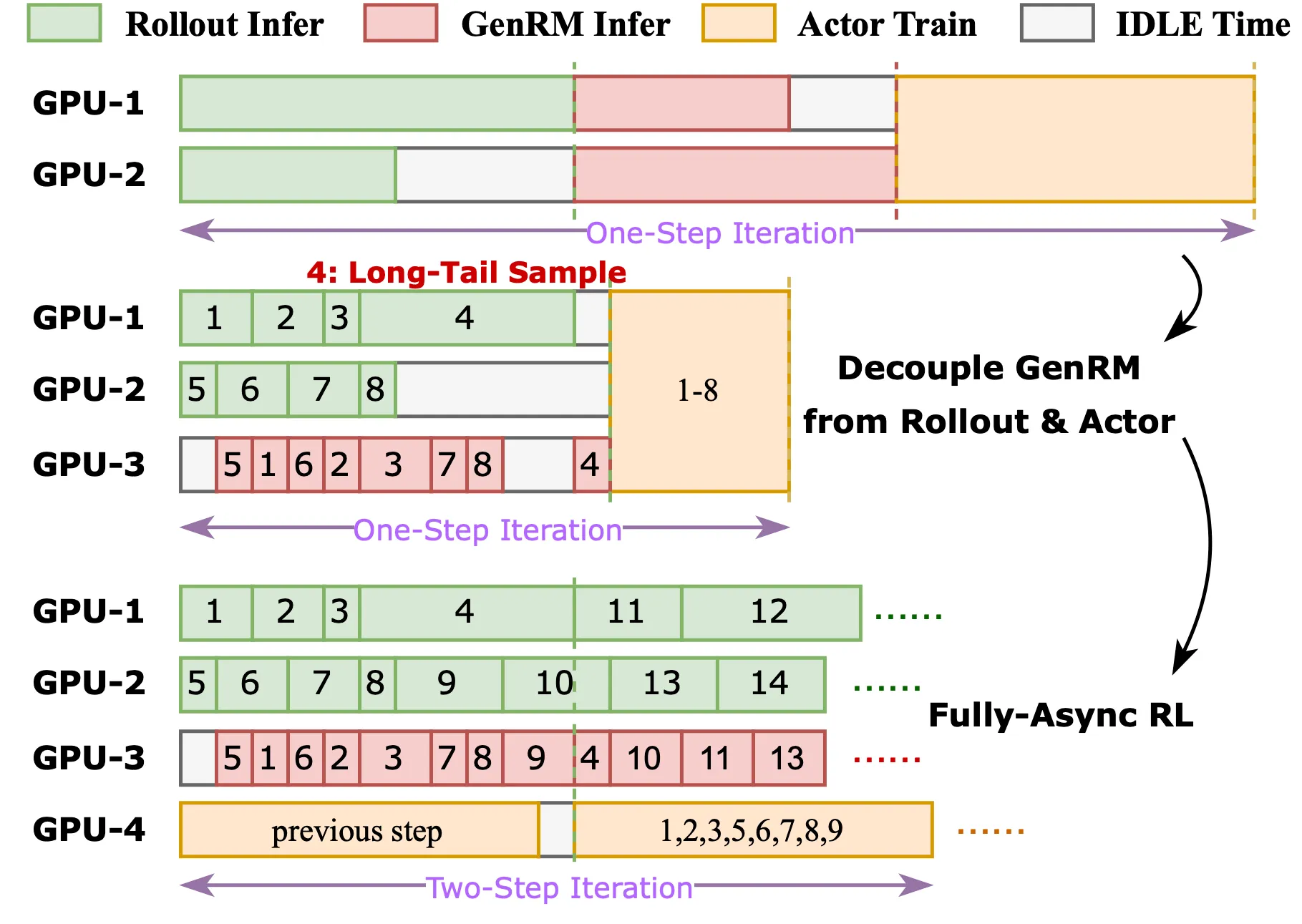
We have also implemented a more flexible and easy-to-use infra design for reward models, which has been added to the veRL repo with details in this doc and will be merged as a key feature in a future release. Welcome to use it!

Let’s start with a recent OpenAI study on LLM hallucinations:

“Language models hallucinate because their training and evaluation processes favor confident guesses over the acknowledgment of uncertainty. Fundamentally, these hallucinations arise as errors in binary classification.”

— OpenAI: Why Language Models Hallucinate

In the context of reinforcement learning, we refer to these “confident guesses” as “flawed positives”, where such flawed guessing rollouts are treated as confident positive signals for policy optimization, thereby reinforcing unreliable reasoning patterns. In this work, we dive into this dilemma, and propose Flawed-Aware Policy Optimization (FAPO), demonstrating the great potential of acknowledging and penalizing these uncertain or flawed patterns to ensure efficient and reliable reasoning.

Distribution and Impact of Flawed Positives in RL

Key Ovservations:

Flawed Positives are Prevalent in Initial Checkpoints (Figure a): Flawed positives are prevalent across various LLMs (Pre-Trained Model, Instruct Model, and Think Model), which stablish the starting conditions for subsequent RL optimization, accounting for 20%–40% of correct rollouts.

Flawed Positives are Stepping Stones in Learning (Figure b): Flawed positives are most prevalent during the early learning stages but diminish significantly as per-sample confidence improves. This highlights their expected role as natural stepping stones in the learning trajectory, allowing the model to initially reach correct answers before gradually evolving the capability to produce fully correct solutions.

Flawed Positives Persist throughout RL Training (Figure c): As the RL training progresses, flawed-positive ratio remains almost constant at around 30%. This indicates that the optimization process struggles to shift from unreliable reasoning to genuine problem-solving.

Flawed Positives Exert Twofold Effects (Figure d): Assigning negative optimization signals to flawed positives yields substantial performance improvements, although the gains appear more gradually in the early training stages. These findings reveal that flawed positives exert a twofold effect: (1) flawed positives act as stepping stones, enabling the model to achieve rapid capability gains in the early stages, and (2) their improper reward assignment can trap optimization in unreliable reasoning.

Flawed-Aware Policy Optimization

Baseline RL setting

Based on GRPO, we also adopt several effective effective strategies such as clip-higher and token-level loss as our standard baseline RL setting.

\begin{aligned} &\mathcal{J}(\theta) = \mathbb{E}_{(q, a)\sim \mathcal{D},\{o_i\}_{i=1}^{G}\sim\pi_{\theta_\text{old}}(\cdot|q)} \\ &\;\;\frac{1}{\sum_{i=1}^{G}|o_i|}\sum_{i=1}^{G}\sum_{t=1}^{|o_i|}\left\{\min \left[\frac{\pi_\theta(o_t|q, o_{<t})}{\pi_{\theta_\text{old}}(o_t|q, o_{<t})}\hat{A}_{i,t}, \text{clip}(\frac{\pi_\theta(o_t|q, o_{<t})}{\pi_{\theta_\text{old}}(o_t|q, o_{<t})}, 1-\epsilon_{l}, 1+\epsilon_{h})\hat{A}_{i,t}\right]\right\}. \end{aligned}

where

(q, a)

denotes a question-answer pair sampled from the data distribution

\mathcal{D}

\pi_{\theta_{\text{old}}}

is the old policy, and

\epsilon

controls the clipping range in importance sampling for stability. The advantage

A_{i,t}

is estimated in a group-relative manner:

\hat{A}_{i,t} = (r_i - \mu_\text{GRPO}) / \sigma_\text{GRPO}, \;\; \text{where} \\ \mu_\text{GRPO} = \text{mean}(\{R_{i}\}_{i=1}^G);\;\; \sigma_\text{GRPO} = \text{std}(\{R_{i}\}_{i=1}^G); \;\; r_i = R_\text{rule}(o, a^*) = \begin{cases} 1, & \text{If}\;\;o = a^* \\ -1, & \text{Otherwise} \end{cases}

where

o

is the predicted final answer of old policy and

a^*

denotes the ground truth.

FAPO-GenRM

We first train a generative reward model (GenRM) to detect flawed-positives accurately and comprehensively, with the following RL reward reformulation:

\begin{aligned} &R_\text{FAPO-GenRM} = R_\text{Outcome} \mathbf{\textbf{+} R_\textbf{Process}} \\ &\text{where}\; R_\text{Outcome} = \begin{cases} 1, & \text{If}\;\;\hat{y}_\theta = y^* \\ -1, & \text{Otherwise} \end{cases} ,\; R_\text{Process} = \begin{cases} - \frac{|\hat{t}_\theta - t^*|}{n}, & \text{If}\;\; \hat{y}_\theta = y^* = \text{FP} \\ 0, & \text{Otherwise} \end{cases}. \end{aligned}

Here,

\hat{t}_\theta

and

t^*

denote the predicted and ground-truth error indices, and

n

is the total number of steps, ensuring

R_\text{Process}\in [-1, 0]

. The process penalty is distance-sensitive: predictions closer to the true error receive higher rewards, while those farther away incur stronger penalties. This design guides the model toward precise error localization and fosters genuine error-detection ability, rather than mere guessing.

FAPO-Reasoning

With the GenRM detecting flawed positives, we then regulate their roles in the final RL optimization. We introduce a reward-penalization mechanism with a group-relative advantage estimation:

\begin{aligned} R_\text{FAPO}&(o, a^*|\theta) = R_\text{RLVR}(o, a^*) \mathbf{\textbf{+} R_\Delta(o,a^* | \theta)}, \\ &\text{where}\; R_\Delta(o,a^* | \theta) = \begin{cases} -\lambda, & \text{If}\;\;\mathcal{I}(o, a^*)\;\text{and}\;\hat{y}_\theta(o, a^*)=\text{FP} \\ 0, & \text{Otherwise} \end{cases}, \\ \hat{A}_{i,t} &= \left[r_i - \text{mean}(\{R_{i}\}_{i=1}^G)\right] / \text{std}(\{R_{i}\}_{i=1}^G). \end{aligned}

Theoretical Analysis about FAPO Effectiveness

We demonstrate the whole learning process and how FAPO leverage flawed positives. The advantage estimation of FAPO can be formulated in that of GRPO:

\begin{aligned} \begin{cases} \mu_\text{FAPO} = \mu_\text{GRPO} - \lambda\gamma \\ \sigma_\text{FAPO}^2 = \sigma_\text{GRPO}^2 + \lambda \gamma(1-\gamma) (\lambda - \frac{4}{\alpha / \beta + 1}) \end{cases} \end{aligned}

where

\alpha, \beta, \gamma

denote the positive rate, negative rate, and flawed positive rate, respectively, and we propose

\rho = \frac{\alpha}{\beta}

to represent the current learning progress.

\begin{aligned} \hat{A}_\text{Flawed} = \frac{1 - \lambda - \mu_\text{FAPO}}{\sigma_\text{FAPO}} < 0 \; \Leftrightarrow \; \lambda > \frac{2\beta}{\alpha + \beta} = \frac{2}{\alpha / \beta + 1} \; \Leftrightarrow \; \rho = \frac{\alpha}{\beta} > \frac{2}{\lambda} - 1 \end{aligned}

The scaling factor

\sigma_\text{FAPO}^2

changes over

\sigma_\text{GRPO}^2

when:

\begin{aligned} \sigma_\text{FAPO}^2-\sigma_\text{GRPO}^2 &= \lambda \gamma(1-\gamma) (\lambda - \frac{4}{\alpha / \beta + 1}) \\ \therefore \text{when }\frac{\alpha}{\beta} < \frac{4}{\lambda} - 1 \Rightarrow \sigma_\text{FAPO}^2 < &\sigma_\text{GRPO}^2; \;\; \text{when }\frac{\alpha}{\beta} > \frac{4}{\lambda} - 1 \Rightarrow \sigma_\text{FAPO}^2 > \sigma_\text{GRPO}^2 \end{aligned}

So the optimization direction moves from warm-up to refinement if current learning progress

\rho

exceeds

\frac{2}{\lambda} - 1

. Furthermore, when

\rho > \frac{4}{\lambda} - 1

, the advantage estimation is downscaled to stabilize training. In terms of

\lambda

, we adopt a majority-guided strategy, which yields

\rho_\text{shift} = 1

, further determining

\lambda = 1

Overall, FAPO provides a principled mechanism for guiding the optimization process, aligning with the ideal learning trajectory where the focus initially lies in producing correct solutions when model capability is limited, and naturally shifts toward refining reliability once correct rollouts surpass incorrect ones.

Experiments

FAPO-GenRM

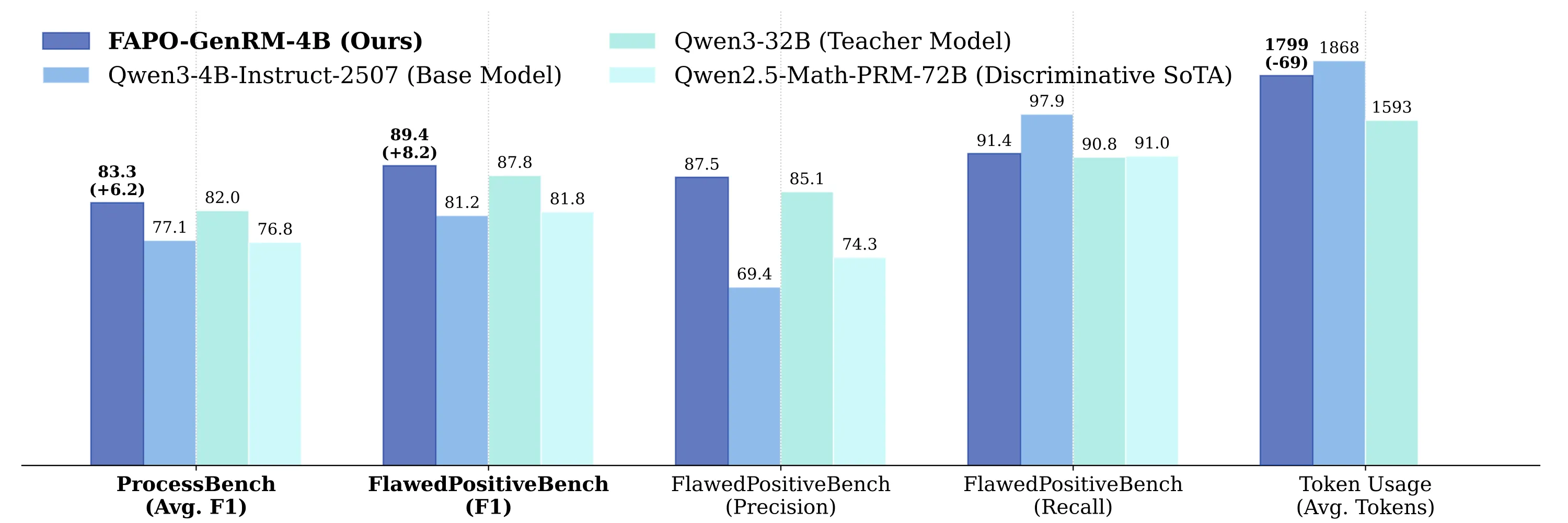
FAPO-GenRM-4B achieves substantial improvements on both FlawedPositiveBench and ProcessBench, even outperforming the teacher model Qwen3-32B, further demonstrating the effectiveness of our approach.

FAPO-Reasoning

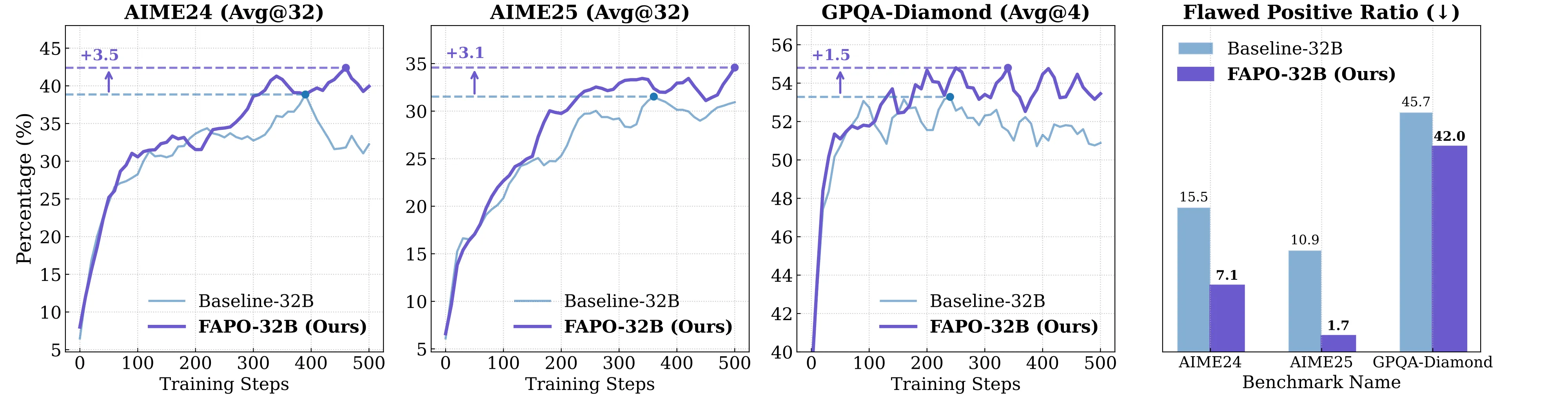
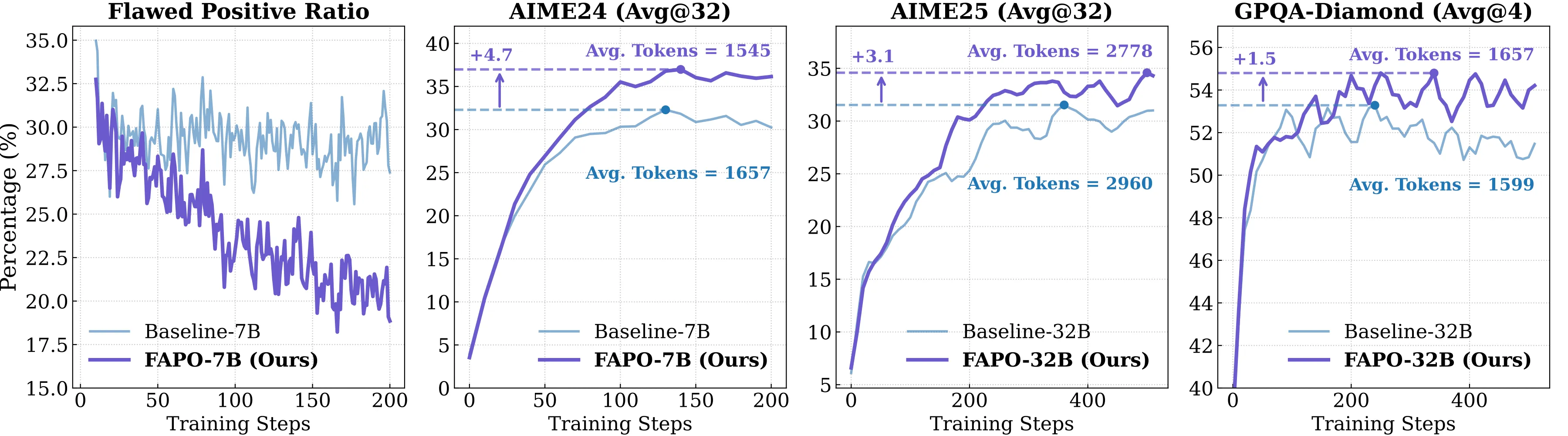
We evaluate FAPO Models in AIME24, AIME25 (Math Domain), and GPQA-Diamond (General Domain), demonstrate the great potential of FAPO in:

(1) Outcome Correctness: FAPO consistently maintains a clear advantage of accuracy over the baselines.

(2) Process Reliability: FAPO responses exhibit a substantially lower flawed-positive ratio.

(3) Training Stability: By mitigating the impact of flawed positives, training stability is enhanced.

Infrastructure design

Introducing generative reward models (GenRMs) may have a considerable impact on the whole RL process, influencing both algorithmic effectiveness and infrastructure efficiency. Below, we outline the following roadmap (part implemented):

[1/N]: Standalone GenRM seperated from Rollout.

[2/N]: GenRM router to distribute request.

[3/N]: Mixture of colocate and standalone mode.

[4/N]: Fully Async RL Pipeline Construction.

BibTeX citation

    
    @article{ding2025fapo,
  title={FAPO: Flawed-Aware Policy Optimization for Efficient and Reliable Reasoning},
  author={Ding, Yuyang and Zhang, Chi and Li, Juntao and Lin, Haibin and Liu, Xin and Zhang, Min},
  journal={arXiv preprint arXiv:2510.22543},
  year={2025}
}